- CIPD level 5HR02 Assignment: Talent Management and Workforce Planning Unit Guide
- Level 3 D/615/3823 Assignment: Regulation, Protection, and Collaborative Practice in Health and Social Care
- ILM Level 4 Assignment 01: Developing Leadership Styles: An Action Plan for Effective Leadership and Team Engagement
- Level 6 Unit T/615/2726 Assignment: Strategic Project Management: Identifying, Planning, and Controlling Projects for Business Success
- EDD-U1-T4 Assignment: Internal and External Support Services for Educational Practitioners
- Discussion Paper on Market Forces and Government Interventions for Business Leaders
- Unit 10 Customer Relationship Management Assignment – CRM Processes & Stakeholder Roles
- CIPD 7HR02 Resourcing and Talent Management to Sustain Success
- Athe Level 3 Health and Social Care Assessment Questions
- M/618/4168 Unit 2 Principles, Values and Regulation in the Health and Social Care Sector – ATHE Level 3
- ILM Communication Skills Self-Assessment
- ILM Unit 8600-309: Understand How to Establish an Effective Team
- CMI Unit 525 Using Reflective Practice to Inform Personal and Professional Development
- Understand and Work with a Wide Range of Stakeholders and Organisational Structures – Assignment 1
- Assessment: Financial Performance Evaluation of Savory Snacks Company Ltd for Credit
- CMI L5 Assignment: Managing Stakeholder Relationships: Strategies, Challenges, and Best Practices
- Level 3 Unit 2 Assignment: Principles, Values and Regulation in the Health and Social Care Sector
- COM4006 Assignment: Introduction to Academic Skills and Professional Development
- Assessment: Managing Organisational Change: Evaluating Strategies, Challenges, and Impact
- UNIT CMI 706 Assignment: Finance for Strategic Leaders: The Role, Scope, and Impact of Finance
MAST4001: Explain two different methods to solve a quadratic equation and what is meant by a real root: Algebraic Methods Assignment, UOK, UK
| University | University of kent (UOK) |
| Subject | MAST4001: Algebraic Methods |
Questions
a) Explain two different methods to solve a quadratic equation and what is meant by a real root. For each, describe an instance where it would be appropriate to use this method and give an example calculation.
b) Define the discriminant (sometimes known as determinant) of a quadratic equation and, using your own words, explain how it can be used to determine the number of solutions to the equation. Show example calculations to where one, two, or no real roots are found. Use hand-drawn or software-generated graphs to show the roots of the quadratic and indicate which roots are real.
c) Explain in your own words how to determine whether a geometric series will:
- converge
- diverge
- oscillate Define any algebraic variables you use.
d) Give an example of each type of series and carry out an example calculation to show that it converges, diverges, or oscillates.
You can either print out the document and answer on the sheet, or answer on separate paper. Once you’ve finished, either scan or clearly photograph your answers to upload them to your assignment.
1
2
a) Express x² + 4x – 7 in the form (x + p)² – q, where p and q are integers.
b) Hence, or otherwise, find the coordinates of the minimum point of the curve y = x² + 4x – 7.
3. The quadratic equation x² + (3k + 1)x + (4 – 9k), where k is constant, has repeated roots.
a) Show that 9k² + 42k – 15 = 0.
b) Hence find the possible values of k.
4.
a) Find the binomial expansion of (2 + 3x)5, simplifying the terms.
b) Hence find the binomial expansion of (2 + 3x)5 – (2 – 3x)5
5.
a) Evaluate and simplify the following logarithm to find x 2logb 5 + ½ log 9 − log 3 = logo x
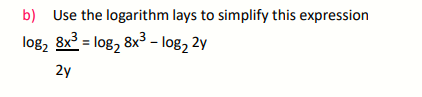
c) The formula for the amount of energy E (in joules) released by an earthquake is E = (1.74 × 1019 × 101.44M) where M is the magnitude of the earthquake on the Richter scale.
i. The Newcastle earthquake in 1989 had a magnitude of 5 on the Richter scale. How many joules were released?
ii. In an earthquake in San Francisco in the 1900s the amount of energy released was double that of the Newcastle earthquake. What was its Richter magnitude?
6.
The first term of an infinite geometric series is 96. The common ratio of the series is 0.4.
a) Find the third term of the series.
b) Find the sum to infinity of the series.
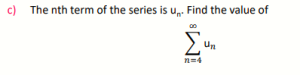
7.
An arithmetic series has first term a and common difference d. The sum of the first ten terms of the series is 460.
a) Show that 2a + 9d = 92.
b) Given also that the 25th term of the sequence is 241, find the value of d.
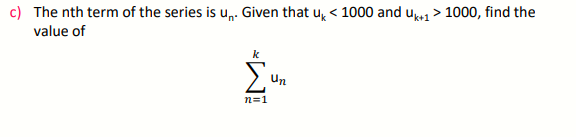
Buy Answer of This Assessment & Raise Your Grades
Are you a UK student studying at the University of Kent (UOK) and facing challenges with your MAST4001: Algebraic Methods assignments? We understand the difficulties you may encounter, and that’s why we offer professional help with assignments. Our expert team is well-versed in the subject and can provide you with personalized guidance. Whether you’re struggling with solving quadratic equations using different methods or comprehending the concept of real roots, our professionals are here to assist you.
Answer
Do You Need Assignment of This Question
