MATHS4102: Effective heat transfer is essential for energy systems. In a smooth channel, heat transfer is achieved by forced convection: Fluid Mechanics Assignment, UOG, UK

Effective heat transfer is essential for energy systems. In a smooth channel, heat transfer is achieved by forced convection. Relatively easy in manufacturing and assembling, corrugated channels with ribs on the walls have been widely used to enhance heat transfer by increasing the surface area. The corrugation configuration impacts both thermal and hydraulic characteristics of the channel flow, which can be quantified by the Nusselt
number 𝑁𝑢 and the pressure drop Δ𝑃, respectively. Different rib shapes have been used and effects on heat exchange investigated. In this study, we will investigate the effects of ribs in a rectangular shape on turbulent heat transfer in a corrugated channel.

Figure 1 presents the two-dimensional cooling channel. The length and (half) height of the channel are 𝐿 and 𝐻, respectively. For the corrugated channel, three equitized ribs are placed in the middle of the channel and attached to the cooling wall. The distances of the rib set to the inlet and outlet are therefore equal and both 𝐷 (see Fig. 1). The length and width of a rib are 𝑎 and 𝑏, respectively. The space between two ribs is 𝑐. A unique set of parameters 𝑎, 𝑏, 𝑐, and 𝐷 will be set up for each student. The other parameters are common. 𝐿 = 50 mm and 𝐻 = 5 mm. The velocity and temperature of the hot air flow entering the channel are 𝑈0 = 50 m s -1 and 𝑇0 = 500 K, respectively. The temperature of the cooling wall is 𝑇𝑤 = 300 K. Symmetric conditions are to be used for the top boundary of the domain.

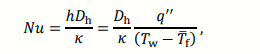
where ℎ is the heat transfer coefficient (W m-2 K-1 ); 𝐷h is the hydraulic diameter (m); 𝜅 is the thermal conductivity of air at 𝑇0. 𝜅 = 33.45×10-3 W m-1 K-1 . ℎ is determined by ℎ = 𝑞 ′′/(𝑇𝑤 − 𝑇̅ f), where 𝑞′′ is the (average) heat flux (W m-2 ); 𝑇̅ f is the volume-averaged fluid temperature (K). 𝐷h = 4𝐴/𝐷wp, where 𝐴 is the cross-section area (m2 ) and 𝐷wp the wetted perimeter (m). In this study, 𝐷h ≈ 4𝐻 = 20 mm.

You are required to complete the following:

1. Perform a mesh independency study on the corrugated channel flow case by using two meshes, one Coarse and the other Fine. Demonstrate the Coarse mesh can produce satisfying results, which are close to the Fine-mesh ones. For this purpose, compare velocity, temperature, and turbulence kinetic energy (TKE) on the Measuring Probe (see Fig. 1), which is 𝐷/2 away from the outlet. You will then use the Coarse mesh ONLY to conduct the following simulations on both the smooth and corrugated channels.

2. Compare the Nusselt number and total pressure loss between the smooth and corrugated channels. Analyze the causes of the differences. Note: in addition to the increased heat transfer surface area due to the ribs, changes to flow characteristics, e.g. enhanced flow turbulence, induced by the ribs are another major cause of the enhanced heat transfer. Investigations and comparisons of TKE and fluid temperature using contour plots are therefore recommended since TKE is an indicator of flow turbulence intensity. Velocity vector plots can be used to investigate whether and how local flow mixing and thus heat transfer have been affected by the ribs.

3. Determine and compare the pressure loss or drop Δ𝑃 between the two cases. Use Total Pressure. Analyze the differences.

4. Analysis and comparison of heat transfer performance among the three ribs and their respective surfaces is expected. Suggestions on further enhancement of the heat transfer based on the analysis are encouraged to make.