- Unit CMI321 Managing Own Personal and Professional Development Assessment | BCU
- CIPD Unit 5CO01 Organisational Performance and Culture in Practice Learner Assessment Brief 2025/26
- ATHE Level 3 Unit 2 How Businesses and Organisations Work Assignment | LCPS
- Unit 531 Principles of Professional Coaching Assessment Brief | SBTL
- PSY4011 Developmental Psychology Assessment Brief – Identity Development in Childhood
- MBA7066 Innovation and Entreprenuership Assignment Brief 2024-2025 | University of Greater Manchester
- Unit 17 Caring for Individuals with Dementia BTEC Level 3 Assignment Brief Case Study
- BTEC Level 3 Unit 15 Care for Individuals with Dementia Assessment
- Unit 3: Professional Practice Authorised Assignment Brief 2025–2026, ESOFT Metro Campus
- Unit 7 Leadership & Management People Assignment – Level 3 Diploma in Business and Management
- HNC Civil Engineering Assignment 2 The Construction Environment
- HNC Civil Engineering Assignment 1 Geotechnics & Soil Mechanics Academic Year 24/25
- UNIT CMI 519 Managing Quality and Continuous Improvement Assessment Brief
- Level 5 in Leadership and Management in Adult Care – Governance and Regulatory Process in Adult Care and Decision Making in Adult Care
- BTM6GSM Global Strategic Management Level 6 Assignment 1 Case Study
- Level 5 in Leadership and Management in Adult Care – Supervising Others and Facilitate Coaching and Mentoring of Practitioners in Care Settings
- Unit 2 Marketing Processes and Planning Assignment Brief 2025-2026
- Unit 805 Strategic Communication Assignment Brief- Media Impact on International Organisations
- UNIT CMI 513 Managing Projects to Achieve Results Assessment Brief
- AFM5CGL Level 5 Corporate Governance and leadership Assignment Case Study
MAST4001: Explain two different methods to solve a quadratic equation and what is meant by a real root: Algebraic Methods Assignment, UOK, UK
| University | University of kent (UOK) |
| Subject | MAST4001: Algebraic Methods |
Questions
a) Explain two different methods to solve a quadratic equation and what is meant by a real root. For each, describe an instance where it would be appropriate to use this method and give an example calculation.
b) Define the discriminant (sometimes known as determinant) of a quadratic equation and, using your own words, explain how it can be used to determine the number of solutions to the equation. Show example calculations to where one, two, or no real roots are found. Use hand-drawn or software-generated graphs to show the roots of the quadratic and indicate which roots are real.
c) Explain in your own words how to determine whether a geometric series will:
- converge
- diverge
- oscillate Define any algebraic variables you use.
d) Give an example of each type of series and carry out an example calculation to show that it converges, diverges, or oscillates.
You can either print out the document and answer on the sheet, or answer on separate paper. Once you’ve finished, either scan or clearly photograph your answers to upload them to your assignment.
1
2
a) Express x² + 4x – 7 in the form (x + p)² – q, where p and q are integers.
b) Hence, or otherwise, find the coordinates of the minimum point of the curve y = x² + 4x – 7.
3. The quadratic equation x² + (3k + 1)x + (4 – 9k), where k is constant, has repeated roots.
a) Show that 9k² + 42k – 15 = 0.
b) Hence find the possible values of k.
4.
a) Find the binomial expansion of (2 + 3x)5, simplifying the terms.
b) Hence find the binomial expansion of (2 + 3x)5 – (2 – 3x)5
5.
a) Evaluate and simplify the following logarithm to find x 2logb 5 + ½ log 9 − log 3 = logo x
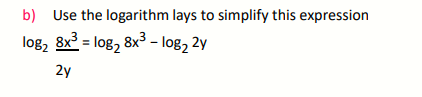
c) The formula for the amount of energy E (in joules) released by an earthquake is E = (1.74 × 1019 × 101.44M) where M is the magnitude of the earthquake on the Richter scale.
i. The Newcastle earthquake in 1989 had a magnitude of 5 on the Richter scale. How many joules were released?
ii. In an earthquake in San Francisco in the 1900s the amount of energy released was double that of the Newcastle earthquake. What was its Richter magnitude?
6.
The first term of an infinite geometric series is 96. The common ratio of the series is 0.4.
a) Find the third term of the series.
b) Find the sum to infinity of the series.
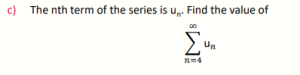
7.
An arithmetic series has first term a and common difference d. The sum of the first ten terms of the series is 460.
a) Show that 2a + 9d = 92.
b) Given also that the 25th term of the sequence is 241, find the value of d.
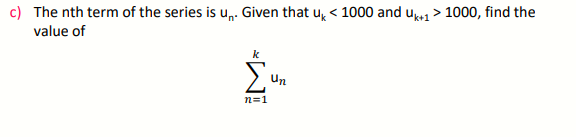
Buy Answer of This Assessment & Raise Your Grades
Are you a UK student studying at the University of Kent (UOK) and facing challenges with your MAST4001: Algebraic Methods assignments? We understand the difficulties you may encounter, and that’s why we offer professional help with assignments. Our expert team is well-versed in the subject and can provide you with personalized guidance. Whether you’re struggling with solving quadratic equations using different methods or comprehending the concept of real roots, our professionals are here to assist you.
Answer
Do You Need Assignment of This Question
